Hypocycloid・・・Trochoid
Parametric representation
x = ( a - b ) cost + c cos (( a - b )/ b
) t
y = ( a - b ) sint - c sin (( a - b )/ b
) t
When one circle rolls (without slipping)
on the inside of another fixed circle,a point
inside or outside the moving circle describes
a curve ,called Trochoid.
a:the radius of fixed circle, b:the radius
of moving circle, c:distance of a point
from the center of movingcircle.
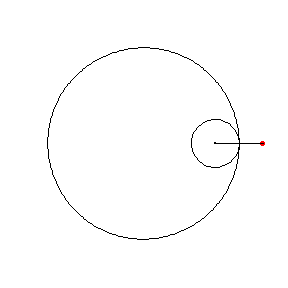
●A point outside the moving circle (if b < c)

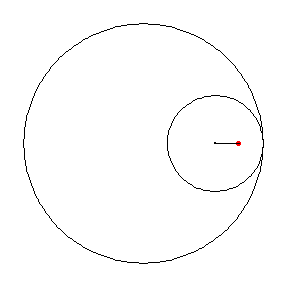
●A point inside the moving circle (if b > c)
※ if b=c,the locus is Cycloid or Deltoid orAstroid.