第1章 Mathematica Tour
Mathematicaとは
Mathematicaは,1988年にStephen Wolframらによって開発された数学・物理や科学技術のための総合的なソフトウェアである.数値計算,記号処理,グラフィックス,プログラミング言語としての機能を備えている.Mathematicaはカーネルと呼ばれる計算を受け持つ部分とフロントエンドと呼ばれるユーザーインターフェースを持つ.この授業ではMathematicaの使い方だけではなく,Mathematicaを活用していろいろな分野(数学,物理,経済,経営など)の問題を考えて行こう.Mathematicaは「数学統合ソフトウエア」としてver3.0以降、入出力のインターフェースが改善され、日本語化にも対応し、学校教育現場においてもかなり使いやすい環境を提供している.そしてさらに,インターネットへの対応も強化されてきている.まずこの章では,Mathematicaはどのようなことができるかをみていく.
1 Mathematica超入門(高級電卓としての活用)
まず,Mathematicaを電卓のように使う方法を紹介しよう.
四則演算
![]()
![]()
![]()
![]()
因数分解
![]()
![]()
![]()
式の展開
![]()
方程式を解く
![]()
![]()
![]()
2 Mathematicaの基本ルール
少し慣れたところで,Mathematicaの基本ル-ルを紹介する.
ヘルプ機能
Mathematicaを扱う際、一番重要なのは「ヘルプ機能を使いこなすこと」といっても過言ではない.ver3からヘルプ機能が充実した。操作中不明なことに出会ったらヘルプで参照するとよい.
Help Browserを使いこなす
組み込み関数を忘れたら

ワイルドカードを併用すると、関連コマンドを検索できる.
![]()
![]()
組み込み関数について
Mathematicaでは,組み込まれている関数や定数はすべて大文字から始まる約束になっている.
Factor, Expand, D, Integarate, Solve, Plot,
ParametricPlot, Sin, Cos, Pi, I, E...
Mathematicaの3種類の括弧
Mathematicaには次のような3種類の括弧があり、数学的に厳密に使い分ける.
![]()
![]()
![]()
カーネルとフロントエンド
Mathematicaの多くは、カーネルと呼ばれる部分とフロントエンドと呼ばれる部分に分かれている.カーネルは実際に計算を実行する部分で,フロントエンドは特定のコンピュータとそのGUI環境に応じて最適化されていて、多くの機種では次に述べるようなノートブックインターフェースを備えている.
キーボードによる効率的な入力例
キーボード操作に習熟している人にとっては、以下の効率的な入力法をマスターした方が早くタイプできると思う.詳細は「ヘルプメニュー」「Help Browser」の「その他の情報」→「キーボードショートカット」を参照のこと.
![]()
![]()
![]()
![]()
ノートブックのスタイルシートを選ぶ
「書式→スタイルシート」には17種類のスタイルシートが用意されていて,好みのノートブックをデザインできる.プレゼンテーションに利用するときなど便利である.
ボタン作成
ボタンは各ユーザーが自由にカスタマイズして使うことができる.
Input →Create Button(入力→ボタンの作成) その際、いくつかの選択がある.まず、pasteを選ぶと次のような空白のボタンができる.
![]()
次に、この空白の中に以下の内容を打ち込む.
![]()
■は : spl : (:は[ESC]キーです)と打ち込むとできる.そしてセルを選択し、Cell→CellProperties→CellActiveをチェックする.(セル→セルのプロパティ→アクティブなセル)すると,セル内にAのチェックが入ればOKである.
![]()
例 式を展開してみよう.
![]()
と入力しマウスでこれを選択・反転し、実行( shift + enter )する.
練習:ボタン作成時の選択をpaste以外も試してみよう.
![]()
ボタンを日本語化することもできる.

![]()
![]()
練習 日本語版因数分解のボタンを作ろう.
パレットを作る
パレットはすでに用意されたものの他、自分で好きなものを作成できる.
Input→Createtable/Matrix/pallete(入力→表・行列・パレットの作成)からパレットを指定し,行列の数を
指定する.(ここでは行2、列2)
これ以降は,先ほどのボタンの作成と同様である.次のように作ってみよう.
そしてセルを選択し,Cell→CellProperties→CellActiveをチェックする.
(セル→セルのプロパティ→アクティブなセル)すると、セル内にAのチェックが入る.
このパレットをノートブックから独立させることも可能である.これを行うためには,パレットのセルを選択し,
File → GeneratePalleteselection(ファイル→パレットの作成)を選ぶ.
![]()
ハイパーリンク作成には、
跳び先のセルを選択→Find→Add /Remove Cell Tags→Cell Tagに名前付けて(勝手な名前でよい)→Add→Close
(検索→セル・タグの追加削除→セルタグに名前付けて追加ボタン→閉じる)
ハイパーリンクを実行する文字列選択→Input→Create HyperLink→Cells with Tag→選択タグをクリック→ok
(入力→ハイパーリンクの作成→タグの付いたセルをチェック→選択すべきタグをクリック→ok)
練習:ボタン作成へ戻るハイパーリンクを作成しよう.
4 Mathematicaでの数の扱い
Mathematicaでは,数を厳密値と近似値とで扱う.整数の計算に関しては、通常は整数型の演算を行うので問題が生じないが,近似値の扱いには若干注意が必要となる.
厳密値と近似値(浮動小数点数)N
Mathematicaでは整数、有理数を厳密値、小数を近似値として扱う.厳密値を近似値に変換するコマンドには N を用いる.その際、演算精度を指定できる.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
厳密値(整数、有理数)の注意
![]()
![]()
![]()
![]()
近似値での注意(機械精度)
![]()
![]()
![]()
![]()
![]()
![]()
N[ ]での精度指定
![]()
![]()
![]()
![]()
![]()
![]()
簡単な例
![]()
| 1.41421 |
| 1.41421 |
| 1.41421356237309504880168872421. |
Mathematicaでの微小数(Mathematicaで、1.0に加算して1.0にならなくなる最小数に関する数)
![]()
![]()
![]()
![]()
ただ浮動小数点数を扱う計算では注意が必要。
例
![]()
| 1 | 3.14159 | 1.22461*10^^-16 |
| 2 | 3.14159 | 1.22461*10^^-16 |
| 3 | 3.14159 | 1.22461*10^^-16 |
| 4 | 3.14159 | 1.22461*10^^-16 |
| 5 | 3.14159 | 1.22461*10^^-16 |
| 6 | 3.14159 | 1.22461*10^^-16 |
| 7 | 3.14159 | 1.22461*10^^-16 |
| 8 | 3.14159 | 1.22461*10^^-16 |
| 9 | 3.14159 | 1.22461*10^^-16 |
| 10 | 3.14159 | 1.22461*10^^-16 |
| 11 | 3.14159 | 1.22461*10^^-16 |
| 12 | 3.14159 | 1.22461*10^^-16 |
| 13 | 3.14159 | 1.22461*10^^-16 |
| 14 | 3.14159 | 1.22461*10^^-16 |
| 15 | 3.14159 | 1.22461*10^^-16 |
| 16 | 3.14159 | 1.22461*10^^-16 |
| 17 | 3.1415926535897932 | 4.9543-4.177*^-26 |
| 18 | 3.14159265358979324 | -4.76-8.1941*^-31 |
| 19 | 3.141592653589793238 | 1.21497-5.7872*^-29 |
| 20 | 3.1415926535897932385 | 1.20641-4.7902*^-29 |
![]()
![]()
![]()
![]()
![]()
![]()
If文ではどうか
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5 Mathematicaでのグラフィックス
Mathematicaは,強力なグラフィックス機能を持っている.
2次元グラフィックス
まずは基本的な2次関数と三角関数を描いてみよう.
![]()
![]()
Plotコマンドにオプションをつけてよう
Plot コマンドのオプションを調べるには、
![]()

上の出力で Mathematica のデフォルト設定がわかる.以下ではこの設定を変更してみよう.
次に,格子枠を入れてみよう.
![]()
今度は,x , y の範囲を指定する.
![]()
3次元グラフィックス
次は3次元曲面を描く.
![]()
3次元曲面の視点を設定する.これには、直接キー入力するよりも,Input → 3D ViewPoint Selectorを使うと便利である.
![]()
軸とボックスを消去する.
![]()
3次元立体
Mathematicaにおいて,3次元の基本的な立体は次のパッケ-ジを読みこむことで実現できる.そのためにまずはパッケージを読み込むことになる.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3次元立体をインタラクティブに動かす
Ver4から次の機能が増えた.これは,マウスで立体を動かすことができる.これにはまずパッケージを読み込む.
![]()
![]()
![]()
6 パッケージについて
Mathematicaには組み込み関数だけでなく,パッケージと呼ばれる一種の外部プログラムが用意されている.これを用いるためにはパッケージを読み込む必要がある.
Clearと=.
Clearは指定されたシンボルの値や定義を消去する.=.は値を消去する.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Remove
Removeは指定されたシンボル自体を除去する.
![]()
![]()
<<
例として立体のパッケージGraphics`Shapes`を読み込んでみよう.
![]()
円錐を描くには,
![]()
Needs
次のようなコマンドNeedsでも読める.多面体のパッケージを読み込んでみよう.
![]()
正12面体を描くには,
![]()
Needs[ "P` " ]と <<P` との違いは, <<p` がパッケ-ジ P がすでに読み込まれて $Packages に含まれていても読み直すのに対し, Needs[ "P`" ]は $Packages に指定されたパッケ-ジが読み込まれていない時のみ読み込むところにある.
読み込み失敗(順序が重要)
パッケージの読み込みは順序が重要だ.ベクトル場を描く関数PlotVectorFieldがパッケージGraphics`PlotField`に入っている.
![]()
そこでパッケージをあわてて読み込む.
![]()
そして再度挑戦する.
![]()
やはり失敗.このような場合は、PlotVectorFieldを除去する必要がある.
![]()
![]()
![]()
![]()
7 アニメーションを作る
Doコマンドでアニメーションを作成する.
![]()
そして、セル全体を選択し、Cell→Animate Selected Graphics(or Ctrl + y )を選ぶ。うまくいきますか?
次のようにすれば改善できる.
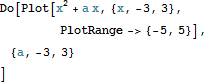
練習:三角関数のグラフのアニメーションを作成しよう.
練習:3次元曲面のアニメーションを作成しよう.