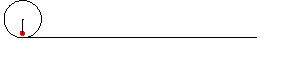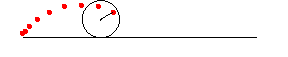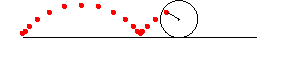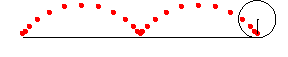
第2章 グラフィックプログラミング
グラフィックス
さて,まず基本的なグラフィックスを復習しよう.
*Plot*コマンド
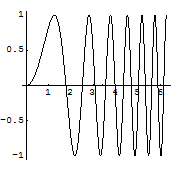
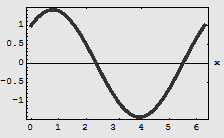
正弦曲線を描く.
In[1]:=
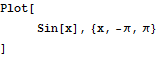
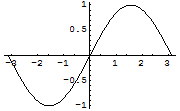
Out[1]=
![]()
複数のグラフを描くにはリスト形式にする.
In[2]:=
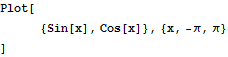
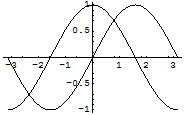
Out[2]=
![]()
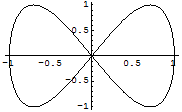
パラメータ表示された曲線は次のコマンド.
In[3]:=

Out[3]=
![]()
練習:Doコマンドを用いて,曲線のアニメーションを作成しよう.
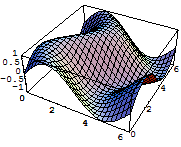
次は3次元曲面.
In[4]:=
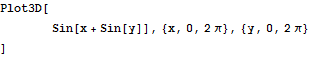
Out[4]=
![]()
練習:Doコマンドを用いて,曲面のアニメーションを作成しよう.
In[5]:=
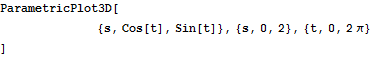

Out[5]=
![]()
以上が基本的なコマンドである.
練習:円錐を作成しよう.
Plotコマンドにオプションをつけてみよう。
Plotコマンドのオプションを調べるには次のようにする.
![]()

次は、x,y軸を等スケールにする.
In[6]:=
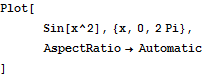
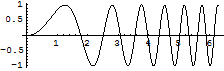
Out[6]=
![]()
プロット枠の縦横比を1:1にする.
In[7]:=
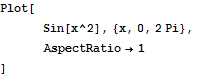
Out[7]=
![]()
格子枠を入れてみよう.
In[8]:=
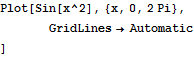
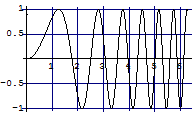
Out[8]=
![]()
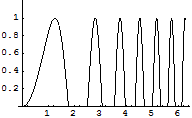
プロットの範囲(yのみ)を指定し、x,y軸の目盛りを設定する.
In[9]:=
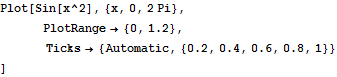
Out[9]=
![]()
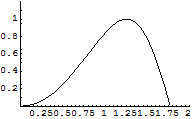
x,yの範囲を指定する.
In[10]:=
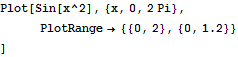
Out[10]=
![]()
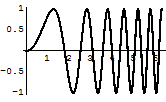
In[11]:=

Out[11]=
![]()
長さ0.01とスペ-ス0.02の破線を指定する.
In[12]:=
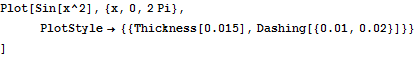
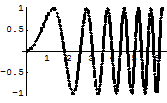
Out[12]=
![]()
グラフに色をつける.(RGBColor[0,0,1],Hue[1,0.9,0.8])
In[13]:=

Out[13]=
![]()
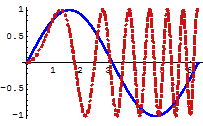
グラフにラベルをつける
両軸にはラベルをつけ、x軸は度数法表示にした.
In[14]:=

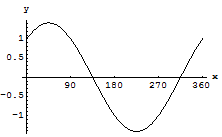
Out[14]=
![]()
In[15]:=
![]()
さまざまなオプションをつけた.
In[16]:=

Out[16]=
![]()
練習問題1:上の三角関数のグラフに,元のSin Cosのグラフを破線で描き加えてみよう.
Plot3Dにオプションをつけてみよう.
3次元曲面の視点を設定する.これには、直接キー入力するよりも、Input→3D ViewPoint Selectorを使うと便利である.
In[17]:=
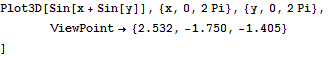
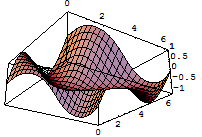
Out[17]=
![]()
ボックスと軸を消し,格子点の個数を変化させる.
In[18]:=


Out[18]=
![]()
照明や陰影のオプションを変える.
In[19]:=
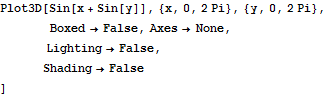

Out[19]=
![]()
In[20]:=

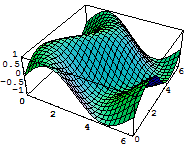
Out[20]=
![]()
密度グラフ(DensityPlot)
デフォルトでの密度グラフである.
In[21]:=
![]()
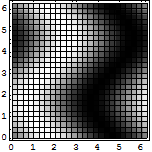
Out[21]=
![]()
いろいろオプションをつける.
In[22]:=

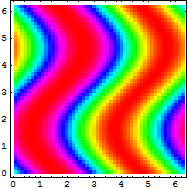
Out[22]=
![]()
等高線グラフ(ContourPlot)
密度グラフと同様な出力を行うが,ここでは2つのGraphicオブジェクトを作成し,それを並べて表示する.左がデフォルトの等高線グラフ.DisplayFunction→Identityは表示抑止オプションである.
In[26]:=

Out[26]=
![]()
右図でいろいろオプションをつける.
In[27]:=

Out[27]=
![]()
GraphicsArrayコマンドで2つの図を並べる.
In[28]:=

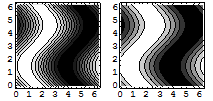
Out[28]=
![]()
2次元グラフィックス・プリミティブ
Mathematicaでの基本的なグラフィックスの生成方法を述べます.これは次の3つの段階からなる.
・グラフィックスプリミティブの生成(用意されているいろいろなプリミティブ)
・グラフィックスオブジェクトの生成(関数Graphics使用)
・表示(関数Show)
このことを円で行う.
Circle
In[29]:=
![]()
In[30]:=
![]()
Out[30]=
![]()
In[31]:=
![]()

Out[31]=
![]()
オプションはPlotlコマンドのときと同様.
In[32]:=
![]()
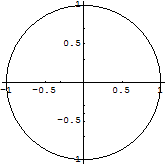
Out[32]=
![]()
In[33]:=
![]()
Out[33]=

その他のプリミティブ(Point,Line,Disk)
基本的な点,線分,円板を描いてみる.
In[34]:=
![]()
In[35]:=
![]()
In[36]:=
![]()
In[39]:=
![]()
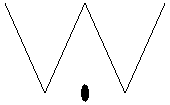
Out[39]=
![]()
オプションをつける.
In[38]:=


Out[38]=
![]()
3次元グラフィックス・プリミティブ
3次元図形を生成するステップも2次元と同様である.
In[50]:=
![]()
In[51]:=
![]()
In[52]:=
![]()
In[53]:=
![]()
Out[53]=
![]()
In[54]:=
![]()
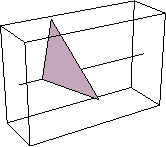
Out[54]=
![]()
In[55]:=
![]()
Out[55]=

In[56]:=

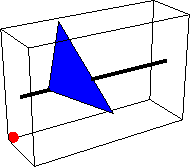
Out[56]=
![]()
練習問題1:円錐を作ってみましょう.また,いろいろ視点を変えて描いてみよう.
プロットの仕組み
In[57]:=
![]()
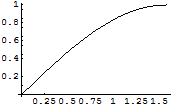
Out[57]=
![]()
In[58]:=
![]()
Out[58]//InputForm=
Graphics[{{Line[{{2.617993877991494*^-7, 2.6179938779914644*^-7}, {0.25488992540742256, 0.25213889196341294},
{0.5328694051959508, 0.5080069997492929}, {0.7939393140028285, 0.7131204212611485}, {1.04500937601917, 0.864929243756943},
{1.1741328775392965, 0.9223551787683757}, {1.2403657810942001, 0.945902740516237},
{1.3122595300248905, 0.9667651045914426}, {1.3813635222545473, 0.9821111970586465},
{1.4117228339769037, 0.9873744690915617}, {1.4451622129766026, 0.9921184097818952},
{1.4766489532819624, 0.9955714086329677}, {1.506146165787852, 0.997910906131906}, {1.5224109849781302, 0.9988296577034247},
{1.5372920787446114, 0.9994387851828285}, {1.545504331691776, 0.9996801745413599},
{1.5498430840253508, 0.9997804888400486}, {1.554468381268543, 0.9998667020589397},
{1.5629353652700015, 0.9999691028010596}, {1.5707960649955088, 0.9999999999999657}}]}},
{PlotRange -> Automatic, AspectRatio -> GoldenRatio^(-1), DisplayFunction :> $DisplayFunction, ColorOutput -> Automatic,
Axes -> Automatic, AxesOrigin -> Automatic, PlotLabel -> None, AxesLabel -> None, Ticks -> Automatic, GridLines -> None,
Prolog -> {}, Epilog -> {}, AxesStyle -> Automatic, Background -> Automatic, DefaultColor -> Automatic,
DefaultFont :> $DefaultFont, RotateLabel -> True, Frame -> False, FrameStyle -> Automatic, FrameTicks -> Automatic,
FrameLabel -> None, PlotRegion -> Automatic, ImageSize -> Automatic, TextStyle :> $TextStyle, FormatType :> $FormatType}]
実はLine文で書かれている.
リストの操作
Mathematicaではリストはもっとも基本的なデータ構造である.Mathematicaにはリストを操作する関数が多くある.特に、グラフィックス、個数の処理、確率を考えるときに便利だ.
リストを作る(その1)
組み込み関数でリストを作る.
In[59]:=
![]()
Out[59]=
![]()
In[60]:=
![]()
Out[60]=
![]()
In[61]:=
![]()
Out[61]=
![]()
In[62]:=
![]()
Out[62]=
![]()
第2引数で刻み幅を指定できる.
In[63]:=
![]()
Out[63]=
![]()
乱数も作成できる.
In[64]:=
![]()
Out[64]=
![]()
練習:Table文で3から31までの奇数列を作ろう.
リストを作る(その2)
多次元配列のリストを作成する.
In[103]:=
![]()
Out[103]=
![]()
複数の反覆子がある場合、その順序は重要である.内側のそれぞれ i に対して、外側の j の値が増加してリストを付け加える.
In[104]:=
![]()
Out[104]=
![]()
行列として表示できる.
In[105]:=
![]()
Out[105]//TableForm=
|
|
||||
|
|
||||
|
|
練習:Tableを用いて {{2,3,4},{3,4,5}}を作ろう.
In[106]:=
![]()
Out[106]=
![]()
In[107]:=
![]()
Out[107]=
![]()
練習:Tableを用いて {{2},{3,4},{4,5,6}}を作ろう.
In[108]:=
![]()
Out[108]=
![]()
リストの大きさ
In[109]:=
![]()
Out[109]=
![]()
In[110]:=
![]()
Out[110]=
![]()
Lengthはもっとも浅いレベルの大きさを返す.各レベルの大きさを見るには Dimensions を用いる.
In[111]:=
![]()
Out[111]=
![]()
リストを操作する
マウスでデ-タリストを取得し,それらを操作する.
In[142]:=
![]()
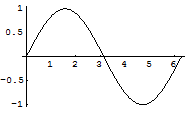
Out[142]=
![]()
グラフィック枠内において,CTRL+マウスクリック(左下に座標が表示される)で点がプロットされる.この状態でCTRL+C,そしてセルにマウスを移動してCTRL+Vとすると,デ-タがインポ-トできる.
In[143]:=
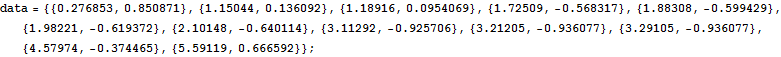
In[144]:=
![]()
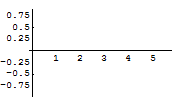
Out[144]=
![]()
In[145]:=
![]()
Out[145]=

In[146]:=
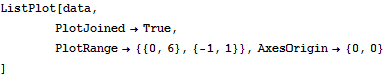
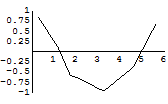
Out[146]=
![]()
多次元配列のリストを操作する.
In[147]:=
![]()
次は,配列の値を高さとする密度プロット.
In[148]:=
![]()
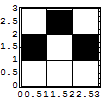
Out[148]=
![]()
次は等高線プロット.
In[149]:=
![]()
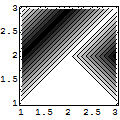
Out[149]=
![]()
次は3次元曲面を生成する.
In[150]:=
![]()
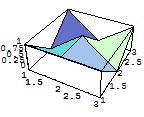
Out[150]=
![]()
以上のようにリストを視覚化できる.これは後の画像処理で詳しく述べる.
練習:自分でリストを作成し、曲面を作成する.
In[152]:=
![]()
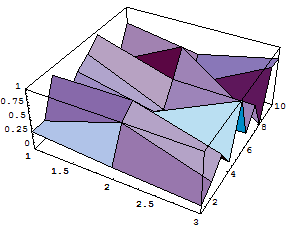
Out[152]=
![]()
Mathematicaでのパターン [ x_ ] (付録)
Mathematicaで関数を定義するときには少し工夫がいる.
In[153]:=
![]()
In[154]:=
![]()
Out[154]=
![]()
これは、記号xのみにしか動作せず、不都合である.これに対し、Mathematicaには,パタ-ンマッチングという考え方があり,x_とすることでパタ-ンに適合する変数に対応する関数ができる.
In[155]:=
![]()
Out[155]=
![]()
In[156]:=
![]()
Out[156]=
![]()
Mathematicaでの等号=と:= (付録)
定義する関数がもう少し複雑になると、さらに工夫する必要がある.
In[157]:=
![]()
In[158]:=
![]()
In[159]:=
![]()
Out[159]=
![]()
=は即時定義(Set) といい、左辺の内容を右辺に代入する.つまり代入の規則を優先して評価するだけである.これに対して、:= は遅延定義(SetDelayed)といい、右辺をすぐには評価せず、Expand[x^2]全体を保持するので、関数が実際に使われるときに初めて評価する.特に:=は関数を定義するときに非常に有効である.
In[160]:=
![]()
In[161]:=
![]()
この辺の詳細は,また後のプログラミングのところで説明する.
いろいろな平面曲線
陰関数表示( ImplicitPlot )
まずパッケージをロードする.
In[162]:=
![]()
In[163]:=
![]()
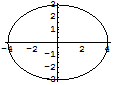
Out[163]=
![]()
パラメータ表示( ParametricPlot )
リストを作成して曲線をプロットする.これは表計算ソフトでの描画方法である.サイクロイドを例に説明します。
In[178]:=
![]()
In[179]:=
![]()
![]()
Out[179]=
![]()
組み込み関数を用いると、
In[180]:=
![]()
![]()
Out[180]=
![]()
もっと一般的にサイクロイドを定義する.
In[181]:=
![]()
In[182]:=
![]()
![]()
Out[182]=
![]()
課題:定数a ,bにいろいろな値を代入して、サイクロイドを描いてみよう.
課題:レムニスケート,カージオイド,シッソイド,トラクトリクス,リマソンなどの曲線を描いてみよう.
In[183]:=
![]()
In[184]:=
![]()
In[185]:=
![]()
In[186]:=
![]()
In[187]:=
![]()
極座標表示( PolarPlot )
極座標系とは,平面上では,原点を基準に1つの動径 r と1つの偏角 θ を対応させる座標系のことである.直交系( x, y )と( r, θ )の関係は,x = cosθ, y = sinθ が成り立つ.
Mathematicaでこれを実現するには,次のパッケージをロードする必要がある.
In[188]:=
![]()
らせんを描くには次のようにする.
In[189]:=
![]()
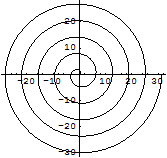
Out[189]=
![]()
次はリマソンの極表示.
In[190]:=
![]()
In[191]:=
![]()
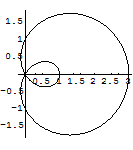
Out[191]=
![]()
課題:定数 a, b, n にいろいろ値を代入して,リマソンを描いてみよう.
アニメーションに挑戦
ここではサイクロイド例に少し高度なアニメ-ションに挑戦しよう.
Append
In[192]:=
![]()
In[193]:=
![]()
In[194]:=
![]()
Out[194]=
![]()
In[195]:=
![]()
Out[195]=
![]()
AppendTo
In[196]:=
![]()
In[197]:=
![]()
Out[197]=
![]()
In[198]:=
![]()
Out[198]=
![]()
今度は,リストが再設定される.この原理をアニメーションに使う.
サイクロイドのアニメーション
次がサイクロイドを表すパラメータ表示.
In[210]:=
![]()
ころがる線分を設定する.
In[211]:=
![]()
接円の中心.
In[212]:=
![]()
接円を設定する.
In[214]:=
![]()
In[215]:=
![]()
In[216]:=
![]()
アニメーション ( 残像つき )
In[217]:=


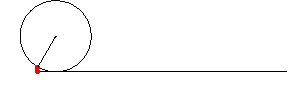
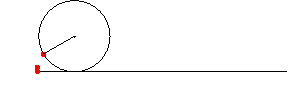
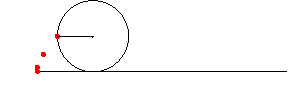
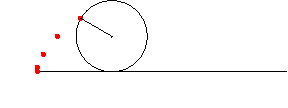

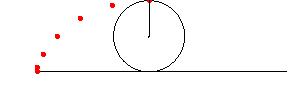
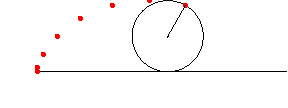


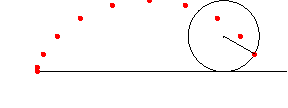
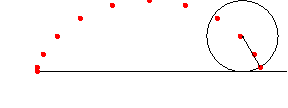
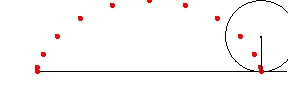
In[218]:=
![]()
In[218]:=
![]()
In[218]:=
![]()
In[219]:=
![]()
リマソンのアニメーション
In[245]:=
![]()
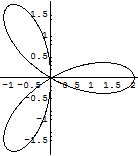
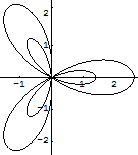
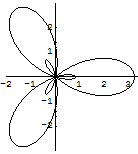
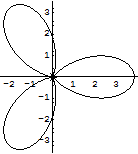
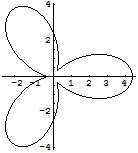
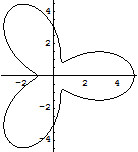
課題:いろいろな曲線のアニメーションを描いてみよう.
いろいろな曲面(Plot3D, ParametricPlot3D)
3次元曲面も平面曲線を描く要領とほぼ同じである.ここではいろいろな曲面を鑑賞しよう.基本的な曲面(球面やトーラス,円錐,円柱など)はパッケージ(Graphics`Shapes`)を活用するとよい.ここではそれ以外の曲面を取り上げる.
放物面
In[221]:=
![]()
双曲放物面
In[222]:=
![]()
猿の腰掛け
In[223]:=
![]()
ホイットニ-の傘
In[224]:=
![]()
8の字曲面
In[225]:=
![]()
3次元曲面を描く.
In[226]:=

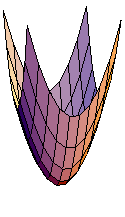
Out[226]=
![]()
課題:いろいろ変数を変えて,オリジナル曲面を描いてみよう.(名前をつけるといいかもしれません)
円錐曲線の切断
円錐を平面で切断してできる曲線を実際にMathematicaで実現させよう.まず、円錐面を媒介変数で定義する.
In[227]:=

次に切断面を定義する.
In[228]:=

xy平面に平行な平面で切断する.(アニメーション)
In[229]:=

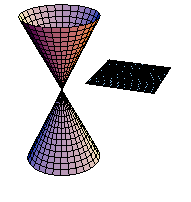
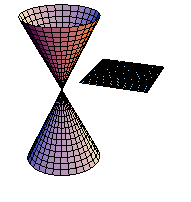
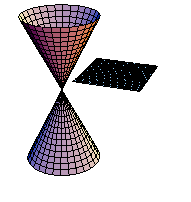
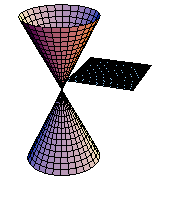
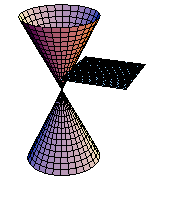
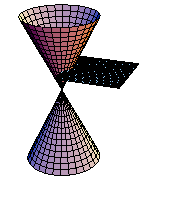
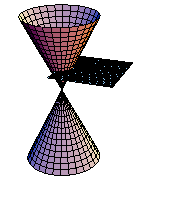
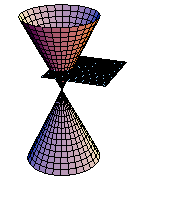
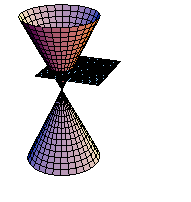
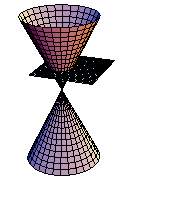
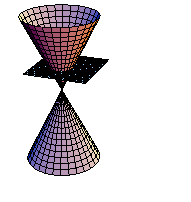
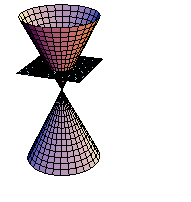
課題:平面をいろいろ変えて、切断面を観察しよう.
Module:局所変数と大域変数
In[230]:=
![]()
これは変数 x が大域変数として値2であると定義している.
In[231]:=
![]()
In[232]:=
![]()
Out[232]=
![]()
In[233]:=
![]()
Out[233]=
![]()
どうしてこうなるかというと,xは依然として2のままであるからでる.
In[234]:=
![]()
|
シンボルの値を解放するにはClearを用いる.
In[235]:=
![]()
In[236]:=
![]()
さらに,Moduleを用いて局所的にのみ有効な変数を定義することができる. (下の式は複合式といって、最後のみ出力する)
In[237]:=
![]()
Out[237]=
![]()
これは大域変数と独立に扱うことができる.
In[238]:=
![]()
Out[238]=
![]()
演習課題1:サイクロイドのアニメーション(発展)
サイクロイドをいろいろ変形するために,変数a ,b でコントロールする関数を作るためには,次のプログラムでは不十分だ.どのように修正すればいいだろうか.
In[2]:=

In[4]:=
![]()
これはうまくいく.しかし,次はうまくいかない.
In[247]:=
![]()
演習課題2: いろいろなアニメーションを作ってみよう.
例:いろいろな図形をいろいろ曲線上で転がしてみよう.
MathematicaのWeb化
gifファイルの生成
簡単なアニメーションを作り、javascript でweb化してみよう.Mathematicaで作成したアニメーションは、ファイル保存形式をHTMLと指定すると、自動的にgifファイル( index_i .gif ) が生成される.
In[242]:=
![]()
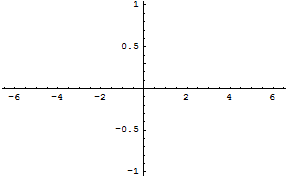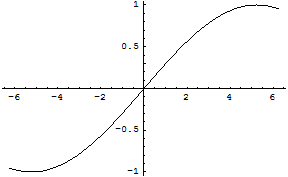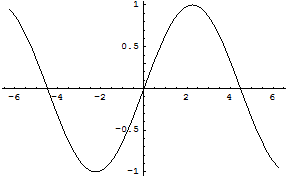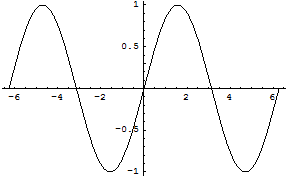
javascriptの利用
javascriptに関しては,別紙資料を参考にして下さい.また、gif アニメーション作成に関しては、専用ソフト(フリーウエアもしくはホームページビルダーのWebアニメータなど)が利用できます.
サイクロイドのアニメーション(発展)
In[243]:=

In[244]:=
![]()