第4章 Mathematica プログラミング
この章では,Mathematicaのプログラミング言語としての側面をみていく.Mathematicaはプログラミング言語としてCやJAVAのような手続き型言語だけでなく,関数型言語,ルールベースト,LISP,Prologのような扱いまで広く対応できる.
手続き型言語とは,プログラミングされた命令を逐次的に実行し,処理の結果に応じて変数の内容を変化させていく.C言語やBASIC、Pascalなどほとんどのプログラミング言語は手続き型言語の構造をもつ.
関数型言語とは,数学的な言語仕様をもつ言語で,計算は計算結果を引数とした関数呼び出しの繰り返しとして行われる.MathematicaやLispが関数型言語に近い特徴をもつ.
1 プログラミングの基礎
Mathematicaでのパターン [ x_ ]
Mathematicaで関数を定義するときには少し工夫がいる.
![]()
![]()
![]()
これは、記号xのみにしか動作せず、不都合である.これに対し、Mathematicaには,パタ-ンマッチングという考え方があり,x_とすることでパタ-ンに適合する変数に対応する関数ができる.
![]()
![]()
![]()
![]()
Mathematicaでの等号=と:=
定義する関数がもう少し複雑になると、さらに工夫する必要がある.
![]()
![]()
![]()
![]()
=は即時定義(Set) といい、左辺の内容を右辺に代入する.つまり代入の規則を優先して評価するだけである.これに対して、:=は遅延定義(SetDelayed)といい、右辺をすぐには評価せず、Expand[x^2]全体を保持するので、関数が実際に使われるときに初めて評価する.特に:=は関数を定義するときに非常に有効である.
![]()
![]()
関数を作る
いままではMathematicaに組み込まれている関数を利用してきたが、ここではユーザーが関数を自作する方法を紹介する.
例として平方関数を作る._はアンダースコアである.
![]()
![]()
引数のパターンを指定することで、区分的に定義された関数を作ることができる.
![]()
![]()
次のように、区分的に定義された関数を通常の数学的表現に近い形で記述できる.
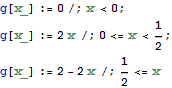
これを図示する.
![]()
条件分岐
IF
二つの条件分岐の時、IFを用いる.第1引数が真であるなら後続の式、そうでないならその次の式が評価される.
![]()
Which
三つ以上の場合の分岐にはWhichを用いる.
![]()
![]()
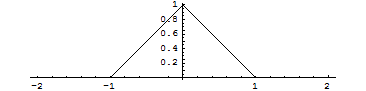
![]()
繰り返し
平方数のリストを色々な方法で作成する.手続き型のプログラミングでは For、Doを用いることが多い.
For
![]()
次は、リスト形式での出力
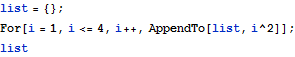
Do
![]()
Nest
関数の反復にはFor、 Doを使うことがある.
![]()
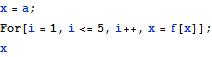
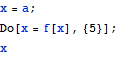
しかし,MathematicaにはNestという強力なコマンドがあり、簡潔な表現になる.
![]()
2 Mapと Apply
Mathematicaをすこし進んだ使い方をしようとする時、是非マスターしておきたいコマンドの一つとしてMapとApplyがある.ともに関数を引数とし、リストを操作する時に用いる.
Apply
リストを用いた計算過程で、f[{1,2,3}]のようにリストに作用させるのでなく、リストの要素に関数を作用させたい時に用いる.
![]()
![]()
和を求める.
![]()
![]()
これは、Applyが式の頭部(Head)を引数に置き換えるからである.
![]()
![]()
![]()
![]()
リストに作用する関数も作ることができる.リストの平均を求める関数を作ってみる.
![]()
練習5:適当な1次元リストを生成して、その平均を求めてみよう.
Map
Mapはリストの要素一つ一つに関数を作用させたい場合に用いる.
![]()
![]()
![]()
![]()
![]()
![]()
これはsinがリスタブルという性質を持っているからだが、一般には成り立たない.
![]()
![]()
![]()
![]()
![]()
![]()
純関数(無名関数)
MapやApplyを用いる場合は適用される関数の名前を指定する必要があった.ここでは関数名を指定せずに関数を引数にすることができる方法を紹介する.
3乗の関数を考える.そのために,まず名前を付ける.
![]()
![]()
![]()
名前を付けずに行うには、純関数もしくは無名関数という考え方を用いる.
![]()
![]()
3 プログラミングによる問題解決
2の平方根の近似値を求める
CやJavaなどの手続き型言語とMathematica言語のとの違いを見ていく.
問題の把握
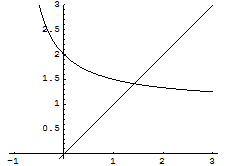
次の関数をもとに,2の平方根に迫る.
![]()
![]()
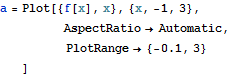
![]()
![]()
![]()
Basicプログラミングでは
*DEFDBL X,Y
INPUT "N=";N
X=1
FOR I=1 TO N
Y=1+1/(1+X)
X=Y
NEXT I
PRINT Y
END *
Forループ
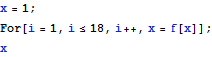
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
関数型に書き換えると,
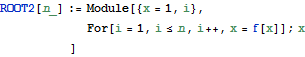
n=18にすると,
![]()
![]()
![]()
Doループ
![]()
![]()
関数型に書き換えるには,
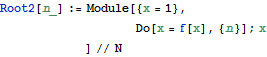
n=10にすると,
![]()
![]()
近似値をリストにするには,
![]()
![]()
Recusive Programming(再帰的プログラミング)
関数として,自分の定義に自分自身を用いる考え方を「再帰的」と呼ぶ.この考え方はプログラミングではよく用いられる.
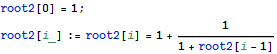
n=10にすると,
![]()
![]()
![]()
![]()
Nest(反復コマンド)
Mathematicaには繰り返しに対して,Nestという便利な関数がある.これは有用である.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
NestListと無名関数を使うことで,
![]()
![]()
![]()
| 1.0000000000. |
| 1.5000000000. |
| 1.4000000000. |
| 1.4166666667. |
| 1.4137931034. |
| 1.4142857143. |
| 1.4142011834. |
| 1.4142156863. |
| 1.4142131980. |
| 1.4142136249. |
| 1.4142135516. |
| 1.4142135642. |
For文でピタゴラス数を求める
ピタゴラス数とは,三平方の定理をみたす自然数のことである.これを求めてみよう.
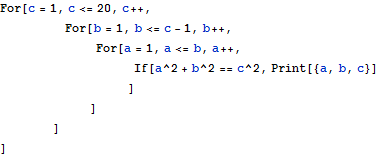
![]()
![]()
![]()
![]()
![]()
![]()
問題 8:関数型プログラムにする.すなわち、nを与えてn以下のピタゴラス数をリストするプログラムを書きなさい.

以下の問題でのプログラミングではMathematicaらしいプログラミングを心がける.
完全数を求める
自然数の完全数とは,その数とその数のすべての約数の和が等しいものをいう.この場合,約数として自分自身は含めない.最小の完全数は6である.これを探すプログラミングを考えよう.
![]()
![]()
![]()
![]()
Divisors[6] から最後の要素を除くには, Drop を使って,properDivisors をつくる.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
問題9 この完全数を求めるプログラムを関数型にまとめよう.
![]()
![]()
![]()
ヨセフスの問題(継子立て)
問題:「ロ-マの兵が10人のユダヤ兵を洞窟に追い込んで,いままさに攻撃をしようとしていた.ユダヤの兵士は敵の刃にかかるよりは自刃の道を選んだ.このとき,伝説によれば彼ら10人は輪になって1人おきに死んだという.最後に死んだのは誰か」
この問題をMathematicaで解いてみる.
![]()
Mathematicaでは,こんな簡単な1行プログラミングでかけてしまう.10人では,
![]()
![]()
途中の経過を出力させる.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
フィボナッチ数
13世紀イタリアの数学者フィボナッチによって研究された有名な数である.
![]()
![]()
と定義すればいい.例えば,
![]()
![]()
![]()
![]()
実はこのプログラミングは,計算に時間がかかる.1度計算した結果に対しても繰り返し計算するため,無駄に時間をとっていまう.このようなときは次のように改善する.
![]()
![]()
と定義すればいい.
![]()
![]()
このような方法は,1度計算したfibb[n]はメモリに記憶することによって,無駄な計算を回避している.
問題 10 フィボナッチ数の話題をもとに,いろいろな三項間漸化式を考察しよう.
collatz 問題(3n+1問題)
この問題は古くから知られている問題で次のようなものである.「ある自然数を考える.これが偶数のときは半分にし,奇数のときは3倍して1足す」このようにして自然数列を定義する.すると,この数列が非常に不思議な振る舞いをすることに気づく.これをMathematicaで確認してみよう.
next[i_?OddQ]:=next[i]=3i+1
next[i_?EvenQ]:=next[i]=i/2
collatz[i_]:=
FixedPointList[next,i,SameTest -> ((#2==1)&)]
9から始めてみよう.
![]()
![]()
あるル-プに入ってしまう.1から30までの様子をみる.
![]()

すべてル-プに入る.
![]()
871もループに入るが,その様子をグラフでみる.
ListPlot[collatz[871],PlotJoined -> True,
PlotRange -> {0,200000}]
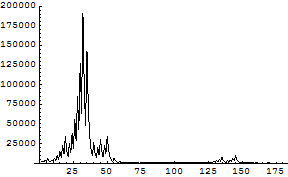
![]()
実はこの規則では,すべて自然数がこのル-プに入りそうなことがコンピュ-タで確認されているが,厳密には証明されていない未解決問題である.とりあえず,100から1000の数がループに入るまでどのくらいの長さか見てみよう.
t=Table[Length[collatz[i]],{i,100,1000}]
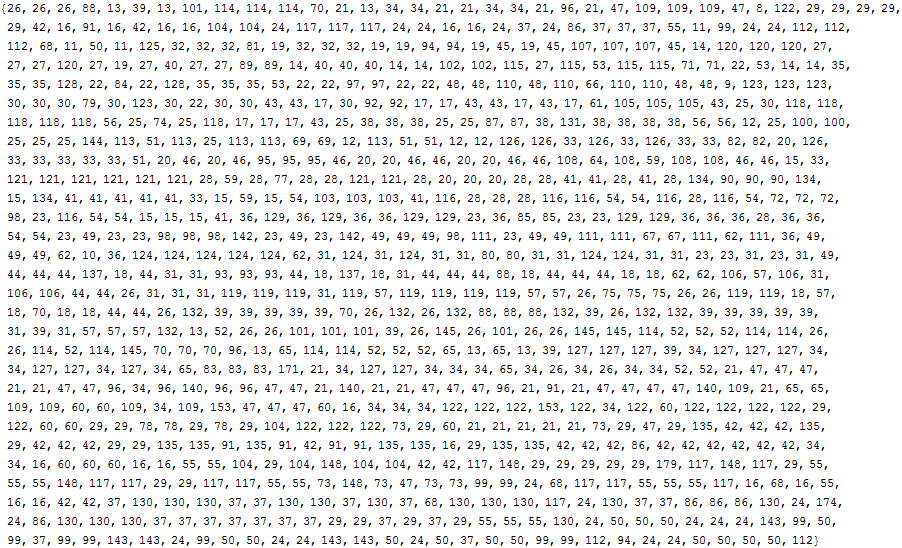
最大の長さは,
Max[t]
![]()
である.そしてこれを与える自然数は,
Position[t,179]
![]()
である.ともかく不思議な数列だ.
タ-トルグラフィックス
タ-トルコマンド
タ-トルグラフィックスとは,プログラミング言語LOGOなどで有名なグラフィックスメソッドである.これはタ-トル(亀)に長さと角度を指定して線分を描いてグラフィックスを描いていくので,このような名前がついた.Mathematicaでは前後左右を次のように定義して,pathのリストを作成する.
![]()
![]()
![]()
![]()
![]()
そして,pathのリストを作成後,Line文で線分を描く.
![]()
![]()
![]()
多角形
正n角形を描くために,次のように関数を定義する.
![]()
![]()
8角形を描く.
![]()
![]()
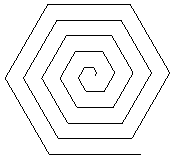
渦巻き線(螺旋)
渦巻き線を描くために,次のように拡大比と角度を次のように定義する.
![]()
![]()
![]()
フラクタル図形
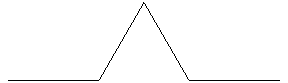
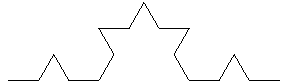
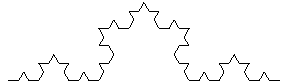
タ-トルグラフィックスを再帰的に使うことで,フラクタル図形を描くことができる.ここでは,コッホの曲線(雪片曲線)を描いてみよう.まずは関数Kochを再帰的に定義する.
![]()

ここで長さ1の線分に対し,その3等分した中央部を正三角形の2つの斜辺で置き換える.この操作を順次繰り返すと雪片のような曲線が描ける.この曲線の特徴はどの部分に注目しても全体と相似形になっていることだ.このような図形をフラクタル図形といい,直線の次元が1次元なのに対し,この曲線の相似次元はlog4/log3=1.2618次元という.
![]()
![]()
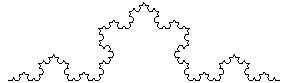
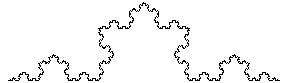
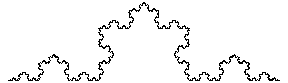
![]()
![]()