第5章 Mathematicaでの数学

ここでは，Mathematicaが扱う数から出発してMathematicaを用いた数学の基本的な扱いを述べる．

１　数の扱い

実数

Mathematicaで扱う数には４つの型，すなわち整数，有理数，実数，複素数がある．これを確認するには関数 Head を用いる．

Head

複数まとめて確認するには,Mapを用いる．

FullForm（内部表現）

また，関数 FullForm でMathematicaの内部表現を知ることができる．

このようにFullFormを用いると,Mathematicaの基本が関数形であることがわかる．

練習　いろいろな式のFullFormを調べよ．

数の精度(Precision)

CやJavaなどのプログラミング言語では,扱える数のビット数が限定される.これとは対照的にMathematicaでは任意の桁数の整数や有理数を扱うことができる．そのことは，精度（precision)をみればいい．Mathematicaではコンピュータに依存する機械精度の演算とMathematica自身のソフトウェアのアルゴリズムで処理する演算とがある．

実数については,一般にその有効桁数に等しい．

これは機械精度である．コンピュータのハードウエアのルーチンで処理できる固定精度の浮動小数点演算である．

練習　次の結果を確認しなさい．

丸め誤差(Roundoff errors)

厳密値でない実数を機械精度で扱うと,丸めによる誤差が生じる．

誤差はこんなに大きくなる．

複素数

Mathematicaでは,複素数を整数や実数とは独立に扱うことができる．

それぞれ実数部と虚数部を求める．

偏角と絶対値を求める．

練習：次のコマンドを実行しよう．

複素数平面

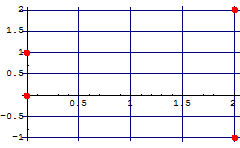
次に，複素数平面上に座標を描く関数を作る．

4点を描く．

高次方程式

次にｎ乗根を単位円周上に描く．

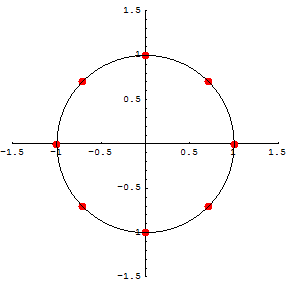
素数

1より大きな自然数で,自分自身と1以外では割り切れないものを素数という．Mathematicaでの素数の扱いを紹介する．

素数の判定と素因数分解

ある自然数が素数であるかどうかの判定は次のようにする．

また,素数でないとき素因数分解は次のコマンドで行う．

10番目の素数は関数 Primeで求められる．

10番目までの素数をすべて列挙するには次のようにする．

次でも同じ結果が得られる．

例題：100までの素数を列挙してみよう．

100までに素数がいくつあるか調べる関数としてPrimePiである．

それゆえ，25番目まで列挙すればいい．

次でも同じ結果が得られる．

素数の分布

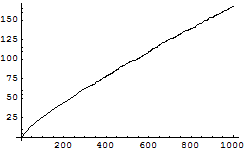
素数の分布は昔から数学では興味の対象であった．

上の曲線がどのような既知の関数で近似されるかは非常に難しい問題だったが,数学者ガウスは次のように予想し,後の数学者がその正しいことを証明した．

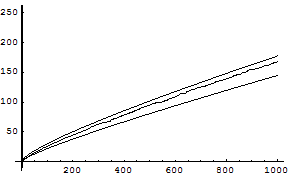
双子素数

素数のなかで連続する奇数のペアを双子素数と呼ぶ．３と５，５と７である．100までにどのくらいあるか調べてみる．

例題：1000までの双子素数はいくつあるか．関数を作成して数えてみよう．twin[n_]  
(ちなみに双子素数が無限個存在するかどうかは数学上，未解決の問題である）

メルセンヌ数

メルセンヌ数とは，の形をした自然数のことをいう．特に素数になる場合メルセンヌ素数といい，最大素数の発見に非常に深い関係をもっている．これに関してはGINPSというプロジェクトがある．

次でも同じ結果が得られる．

メルセンヌ数の素数判定

このメルセンヌ素数が無限個存在するかどうかも数学上未解決であるし,今後，巨大素数の有力な数であることは間違いないだろう．現在は世界中でGINPSにより発見の競争が起こっている．

2 　式の扱い

因数分解（再録）

式の展開（再録）

方程式を解く

このように近似的に解を求めることもできる．次のように連立方程式も解ける．

近似的に解を求めるコマンドには,FindRootがある．これは後で説明するNewton法というアルゴリズムを使っている．

この意味は,x=0を初期値として解を探しにいくことだ．

３ 微分・積分

Mathematicaでは,記号形式で極限や微分・積分の計算が実行できる．

極限

グラフで確認しよう．

左右の極限も計算できる．

微分積分の基本計算

1変数の微分は,

2階の微分は,

合成関数の微分は,

不定積分や定積分は，

パレットを用いると,

複雑な関数の定積分は数値積分で近似値を計算する．

練習   次の微分・積分の計算を行いなさい.

４ 微分方程式

微分積分の応用例として微分方程式を眺めてみよう．この考え方は，自然科学だけでなく社会科学（経済，金融）などにも広く応用される．人工衛星，流体，経済予測，気象予報など未来を予測ために重要なものだ．

１階の常微分方程式

次の例は,変化率 x'[t] が自分自身 x[t] に比例するものである．

このような関数は指数関数になることが分かる.

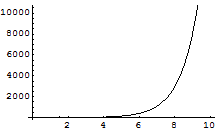
ロジスティック曲線

前の例に,2乗の項を付け加えた．

すると,次のような曲線が現れる．これをロジスティック曲線という．最初は，単調に増えていくが，次第に頭打ちになる関数である．

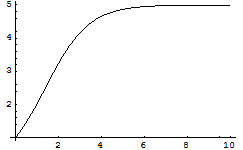
２変数の微分方程式

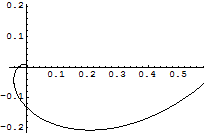
平面のベクトル場

上の様子をベクトル場によって表現するためには,パッケ-ジをまず読み込む．

５　数値計算

Mathematicaで行えるいくつかの数値計算の方法を紹介する．

関数の反復

関数を反復させて数値計算を行うと便利である．この方法はプログラミング上いろいろあるが，MathematicaではNest,NestListという便利なコマンドがある．

Nest,NestList

関数に固有の名前がない場合は、次のようにする．（pure function)

二分法

まず、解が存在する範囲を探す．